涡街流量计的工作原理是什么？

涡街流量计就是利用“涡街”来测量流量的仪表。什么是“涡街”呢？在一定的条件下，当流体绕过一个障碍物继续向前后，旋涡像街灯一样在障碍物的两侧交替排列，因而得名“涡街”。该现象由航天工程学家（同时也是钱学森的导师）冯·卡门（Theodore von Kármán）发现，因此也被称为“卡门涡街”。

图表 1 卡门涡街

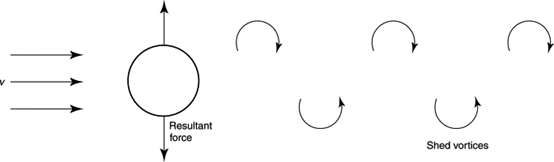
图表 2 卡门涡街示意图

如何利用涡街测量流量呢？当我们用如下关系式来描述管道中卡门涡街的频率f和流体流速v之间的关系时，

假设St为一个正的常数，那么这个式子就是一个线性的关系式，流速v越大，卡门涡街的发生频率f也越快。

图表 3 流速越大，卡门涡街的发生频率也越快

当我们测量出这个频率值f，也就能算出管道中流体的流速v，再根据公式：

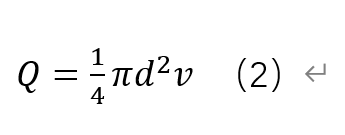
就可以算出体积流量Q了。这就是涡街流量计的工作原理，本文结束。

才怪！（手动鬼脸）

上文遗漏了一个关键信息，我们凭什么假设St是一个正的常数呢？事实上我们并没有一个公式来预先算出St的数值，它就是通过卡门涡街实验来进行测定的。历史上的研究者们在流道中放上不同形状的障碍物，然后让流体在不同速度下绕过障碍物向前流动。经过一次次地测量卡门涡街的频率后，研究者们发现，St的数值只与障碍物的形状和流体的雷诺数（Re）相关。简单来说，Re是用来描述流体流动状态的无量纲数，知道了流体的Re后可以判断它属于层流还是湍流。关于Re的具体含义会在文末介绍，这里先写出它的定义式：

可以看出，Re的数值与流体的流速v密切相关。在不断地试验中研究者们发现，当雷诺数处于一定区间时，St数近似为常数。对于圆柱障碍物（即圆形横截面障碍）而言，这个常数为0.2。

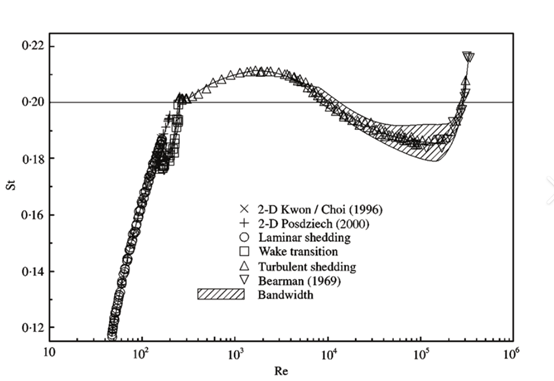
图表 4 圆柱障碍物条件下斯特罗哈数（St）和雷诺数（Re）的实验数据关系

需要注意的是，St与Re的关系并不一定像上图那样是上升趋势，若障碍物的形状不同也可能呈现下降趋势，St数为常数的区间也会随着障碍物的形状而改变。卓然天工涡街流量计采用的是三角柱障碍物（即截面形状为类三角形），底边朝向流体的来流方向。

图表 5 卓然天工FMVT200-DN50带温压补偿涡街流量计

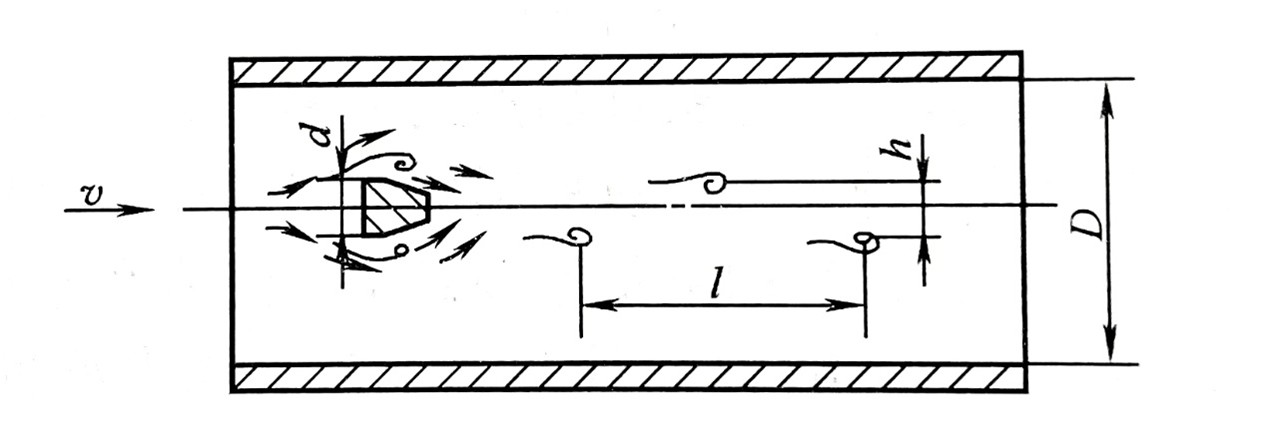
图表 6 三角柱卡门涡街

此结构下的St数和Re数的关系如下图所示，线性测量区域下限要求Re＞4000，上限值则需要查表确定。

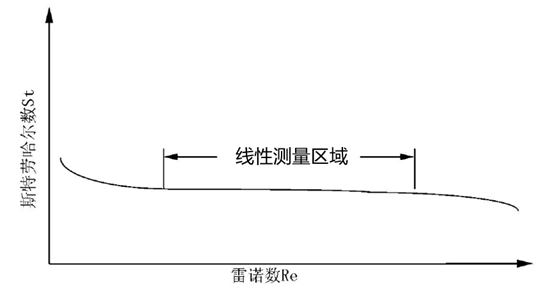
图表 7 涡街流量计的线性测量区域

当管道中流体的Re数值处于线性测量区域中时，卓然天工涡街流量计利用压电传感器检测涡街带来的流体压力波动并得出涡街的频率f，再根据式（1）和（2）就可以算出管道内的流速v和体积流量Q了。

什么是雷诺数（Re）？

雷诺数（Re）是一个用来描述流体流动状态的无量纲数（类似的无量纲数还有很多）。光凭直觉我们就能想象出，流体的流动状态与流速紧密相关，当管道中的流体流速较慢时，整个流动状态平稳、恒定。

图表 8 透明的层流水柱

而当流速变得很快时，流体的流动状态就会变得剧烈、紊乱。

图表 9 剧烈的湍流水柱

不同种类的流体究竟在什么情况下才会由层流逐渐转变成湍流呢？英国物理学家雷诺（Osborne Reynolds）结合流体的密度、流速、粘度和管道的直径四个参数得到了一个无量纲（即没有单位）的数，并在实验中发现此数能很好地估计实际管路中流体的流动状态。这个数就被命名为雷诺数（Re）：

（3）

无论何种流体，只要我们能算出它在流动时的Re数，就可以知道它实际流动时究竟是层流还是湍流。通常我们认为Re＜2000时为层流，Re＞4000时为湍流，处于二者之间时为层流到湍流的过渡形态。

在物理意义层面上，雷诺数可以被认为是流体流动过程中惯性力和粘性力的比值。当雷诺数很小时，流体的流动状态像是管中心的高速层一层一层地“粘”着流体往前移动，越靠近管壁的流层流速越低（毕竟管壁是静止不动的），流体整体呈现层流状态；而雷诺数很大时，惯性力占主导地位，各流层之间相互干扰，微小地旋涡、回流充满了整个流道，流体整体呈现湍流状态。

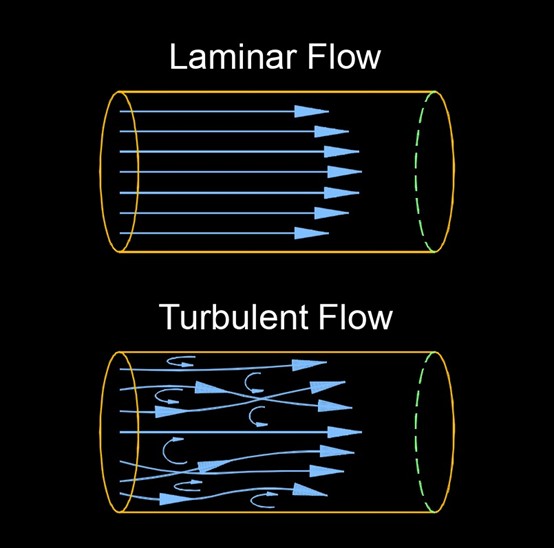
图表 10 层流（Laminar Flow）和湍流（Turbulent Flow）的流速分布